Hopefully everyone’s gotten a chance to look at the setup for the problem here. I got 2 great comments, so it looks like I have something to talk from.
So there are a couple different options here. Being Magic, there are a lot more option here than what I’m presenting, but we’ll narrow the focus down to what actually seems to matter. Your main choices are:
- Swing with Knight of Meadowgrain, leave mana open for harm’s way
- Play Honor of the Pure, swing with Knight of Meadowgrain
- Don’t swing, maybe do something post-combat
There are a few more combinations throwing in the Figure of Destiny somewhere (I should probably switch out the figure for a 2 mana creature so that + harm’s way isn’t an option, but no worries), but as far as the outcomes I listed, that really shouldn’t affect it.
On this turn, only 1 red mana open and an unknown card means your opponent is representing Lightning Bolt. We can throw this together into a table to see what we get (too lazy to do the HTML on it, sorry)
The numbers inside are our payoffs, normalized so I don’t have to use decimals. See the original post for how those numbers correspond to the payoffs, and see Salivanth’s comment for more explanation on all of those (the only one I disagree with is the swing, no bolt situation. He might play maelstrom pulse, not Jund Charm, so you that’d be a 50%er as well)
What do we have here? Well, we learned about dominant strategies in the last “You Make the Play“, so we can try to apply that first. Remember, a strategies dominates another if it results in a better outcome regardless of what your opponent does (here’s a little more: a strictly dominant strategy always does better; a weakly dominant strategy does at least as well in all situations). Looking at the chart, we can see that not swinging is a dominated strategy. Swinging only results in payoffs of 3 regardless of bolt, and doing nothing has 2s regardless of bolt, so you’re always better off swinging. If you want to take a look at Salivanth’s comment again, he shows that HotP is strictly dominated by no HotP, which I agree with up to the point about what happens in scenario 2.
Now if we only had dominant strategies, this would be where the story ends. If your opponent does have a bolt, we shouldn’t play HotP, but if they don’t, we should play HotP. In the end, this should be pretty obvious, but is a lead-in into how we determine what we do.
Reyemile made the excellent point that whatever we do is “pure guesswork” for the reasons listed. Simply, I haven’t told you anything else about how the game has been going so far. How many bolts has your opponent played? How many cards left in the library? Were there any other times where they clearly should’ve played it if they had it? The most important point here is that the best action is determined by what you think your opponent has in your hand.
Again, not surprising, but remember what happened in the Prisoner’s Dilemma. Sure, it matters what your opponent does in figuring out your payoffs, but it doesn’t affect what you should do; you should accuse the other person (or in our Magic case, sit). Here, what you’re trying to do is figure out what your best response (that’s official terminology) is to your opponent’s action.
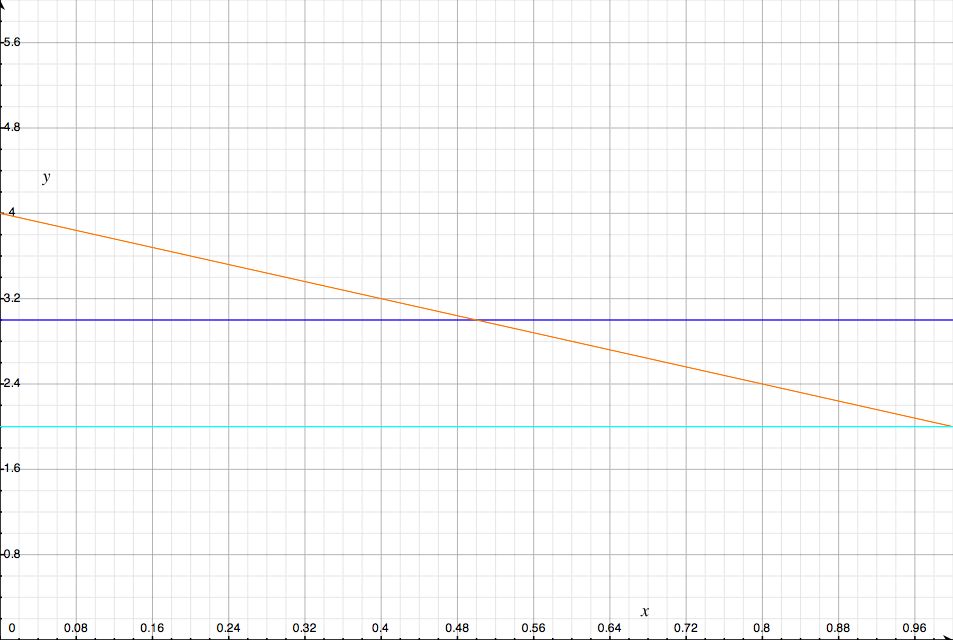
And this should be intuitive as well. Depending on how confident you are about what your opponent is going to do. Basically, we can multiple the probability that your opponent has a bolt by the payoffs for each action you choose. Thus, we get equations about the expected payoffs for various actions at various confidences. Here’s a graph about what that looks like. The x axis is your judged probability that they have a bolt. y axis is payoff. Blue line is swinging only, orange line is HotP, and teal line is doing nothing.
(Major props to Apple, by the way, for having the Grapher application. That was really easy)
So what you see there isn’t surprising. Doing nothing never yields the best reward, and HotP is only better when they don’t have a bolt. In more Game Theory terms, nothing is strictly dominated by swinging and weakly dominated by HotP. Swinging only is better when you think there’s a greater than 50% chance that your opponent has a bolt. This, of course, is on the graph because you can look for the intersection between the two curves and determine the ranges in which one is greater than the other. The result is a little trivial in this case because it happens at 50%, but when I get this into a real slide, I’ll pick more creative payoffs so that the intersection is at 57% or something.
So that’s about it with best response. As foreshadowing, best response is the basis for one of the more famous results in Game Theory named after a dude with a movie now, so maybe we’ll hit that if I can come up with a half decent example. And I’ll put responses to the comments from last time more fully in another comment there. Of course, feel free to comment again on this one. I feel like I’m almost hitting the point of BSing here to try to work this in, so if you’re disgusted by this, please don’t just run away. Let me know; criticism is great feedback.
Tags: bestresponse