Archive for July, 2009

Swans at the Monte Carlo

Thursday, July 23rd, 2009

Looking around on the internet, I found a few interesting articles doing hard stats work on magic. Pretty consistently, though, instead of doing combinatorial (is that a word?) analysis, they just ran a monte carlo simulation to determine what happens. Having just taken a class on probability, I thought I would try to do some deck analysis the definite, combinatoric way. And then I realized it was hard, so I did a monte carlo simulation as well.

Monte Carlo simulations are named after the casino, though I’m not entirely sure why. The basic idea of it is that often, you have problems you want to solve that either don’t have closed forms or have very complex closed forms (closed forms are expressions that are finite and well-defined. Sorry that’s vague, but I’m not entirely sure what the official definition is either). In the case of Magic, I’m pretty sure closed forms exist to express what sequence of cards you draw and how winnable certain orderings are, but they’re hard. Instead, one can find an approximate solution by running a very large amount of simulations of the problem and determining the answer at the end by averaging over all of those answers.

One place where this can be applied in Magic is to determine when a deck can win. One deck that’s come out of nowhere recently is cascade swans. The deck basically works by combining seismic assault with swans of bryn argoll and a lot of lands. Once you get both cards out, you start whacking your own swans to draw lots of cards, then pitch a bunch of lands to do damage to your opponent. Fun. It got cool when Alara Reborn was printed because cascade cards effectively increase the number of copies you have of each of those cards. So it’s a combo deck, and when the pieces are down, it goes.

There are a couple reasons why I decided to do an analysis of this deck. First, it’s simple. Barring lands (which I kind of ignore because they’re hard), there are only 5 different cards. Because it’s a combo deck, you know exactly when it wins. Two, it’s very non-interactive. Pre-sideboarding, it doesn’t really bother to do anything with or to your opponent other than spontaneously win. The simulation works really well as a goldfish to make it simpler. Three, I was curious to see how the deck works, because I’ve actually never played, played against, or even seen it played in a youtube video. It seems like an easy deck to play, too, unlike, say, sunny-side up, so that would make it easy to program.

To make this work, I threw together a python script that plays a swans deck. It has some pretty simple logic on making choices, and actually punts on most of Magic. But I figured that’s okay. So here’s a look at a couple sample runs.

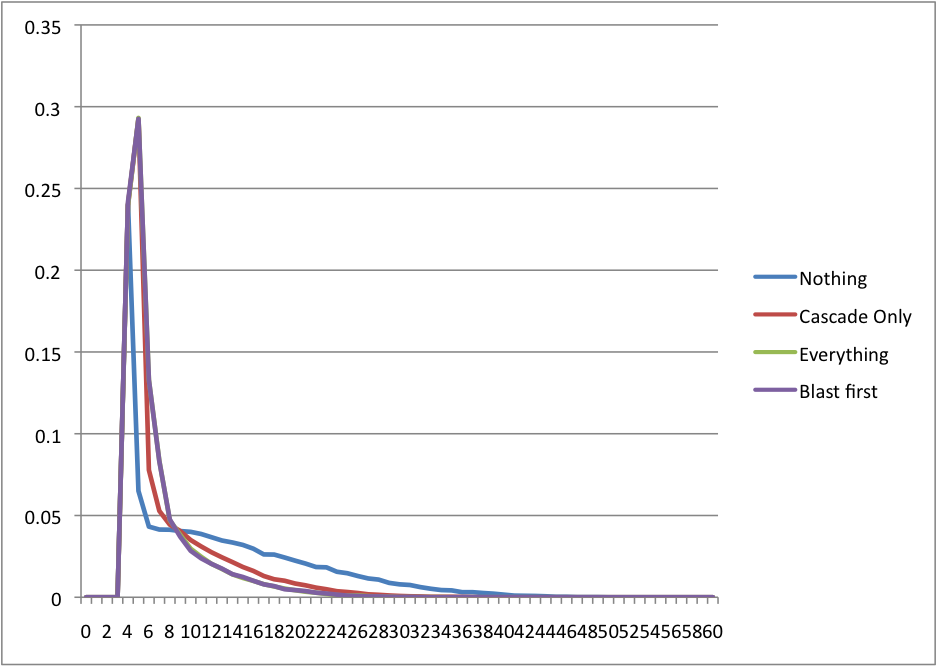
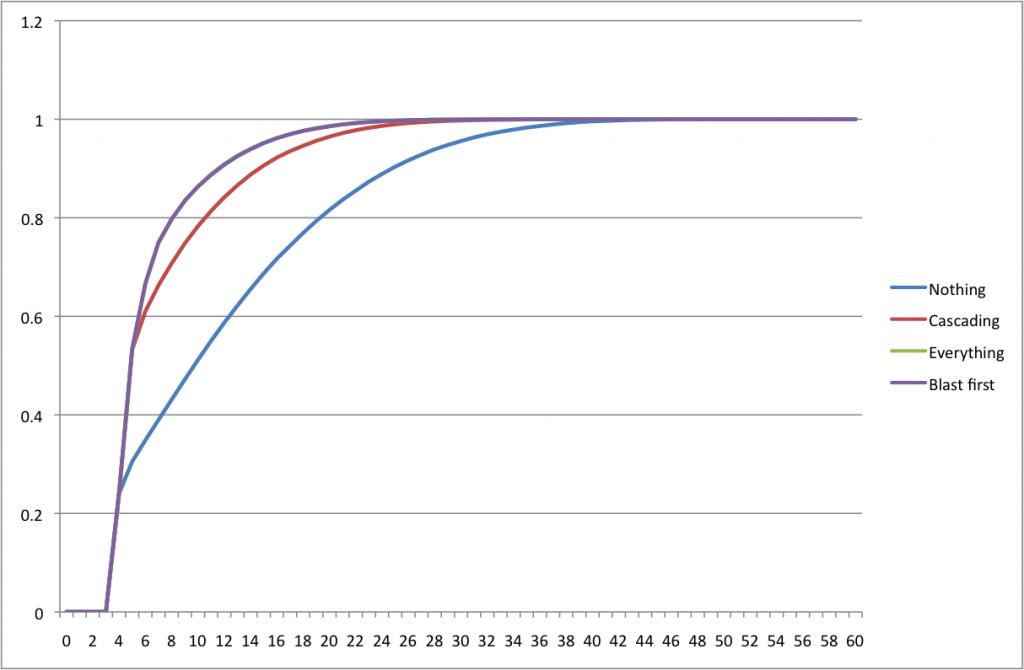
I ended up programming it in steps to make sure it worked all the way along, and that actually gives us some interesting analysis. Over 100,000 runs, I compiled how many times the deck won on that turn in 4 cases. 1) Assuming Ad Nauseam and Cascade are dead cards and do nothing 2) Cascade works, but Ad Nauseam doesn’t 3) Both work, and Bloodbraid Elf is preferred to be played before Bituminous Blast and 4) Both work, and Blast before Elf. Here are 2 graphs on it. The first is how often it was won on that turn, and the second is cumulative (meaning how often it won by that turn)

Swans data

>>> swans.playGame()
DECK
Land Land Land Land Land Land Land Land Land Land Land Land Land SwansofBrynArgoll SeismicAssault Land Land BituminousBlast Land Land BituminousBlast Land BituminousBlast BloodbraidElf Land Land Land Land SeismicAssault AdNauseam SeismicAssault SwansofBrynArgoll Land BloodbraidElf SwansofBrynArgoll Land Land Land Land Land BloodbraidElf Land SeismicAssault Land Land Land Land BloodbraidElf Land Land Land Land Land
HAND
Land Land Land Land SwansofBrynArgoll BituminousBlast AdNauseam
Turn 1
Turn 2
You drew a Land
Turn 3
You drew a Land
Turn 4
You drew a Land
You play SwansofBrynArgoll
Turn 5
You drew a Land
You play AdNauseam
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a Land
Off of Ad Nauseam, you drew a SwansofBrynArgoll
Off of Ad Nauseam, you drew a SeismicAssault
Your life is now 13 because of Ad Nauseam
Turn 6
You drew a Land
You play SeismicAssault
You won on turn 6!

swans-cumulative

(there’s some graph-making noobness. sorry)

So some interesting stuff out of that. There’s a 24%ish chance of winning on turn 3 just by playing seismic assault turn 3 and swans turn 4. Just about 53% chance of winning by turn 5 when cascade is turned on, 66% by turn 6, and 86% by turn 10. That’s pretty impressive. There were two things I thought were impressive. One, cascade is obviously huge. Ad Nauseam helps, but it’s really the cascade that makes turn 5 and 6 shine in consistency. Two, there isn’t a significant difference between playing elf or blast first when you don’t have either assault or swans on the table. I guess I could do analysis to figure out whether it should, but the lines are right on top of each other, so it doesn’t seem to matter.

There are obviously some huge issues with the analysis as is, which I know. This includes:

  • No opponent. Of course goldfishing isn’t entirely meaningful
  • I assume that when assault and swans hit the table, you win. This isn’t necessarily true, but I haven’t heard otherwise. If it happens, though, please tell me, and I can stop being lazy and add that to the model
  • It never mulligans, so it’ll keep 7 land hands.
  • Ad Nauseam doesn’t really look for specific cards. It just chugs until it loses about 10 life.
  • And most importantly, I DIDNT ACCOUNT FOR COLORS

There are at least 3 colors in this deck, and more in some other builds. Trip red on assault makes it hard to get other stuff out, so this isn’t entirely fair. Admittedly, I think this sort of analysis is most valuable when figuring out if you’re getting the right colors, but that takes a lot more work that I wasn’t willing to do, since I figured this would be a quick and dirty script.

If you have any programming knowledge, please take a look at the script. I likely made some mistake, and I would definitely be willing to fix that. Even if you don’t program, it’s python; it’s supposed to read pretty much like english anyways, so take a look. And if you have any ideas about how I can make the script more powerful/inclusive or any other analysis that you think might be useful, feel free to leave a comment.

(edit: I guess I should throw out the caveat that this is very much a work in progress. I plan on iterating this a lot before presenting it, so please, any criticism will be good. Particularly, if you’ve actually played swans before, it would be helpful to just get some idea how it’s played. For example, I assumed that swans players prefer to play, not draw, first, and that there’s generally an order to which cards are played. Let me know if there are any more nuances to playing that I could potentially include)

Posted in Statistics | No Comments »

You Make the Play: Star Edition Take 2

Monday, July 20th, 2009

So I got one great response to the problem. Unfortunately, I guess I should’ve clarified one part of the problem. When I make these posts about game theory, I’m working under the assumption that all else is equal, which is better known as ceteris paribus if you want to sound smart. In this case, you would assume that nothing else not specified in the problem description would remain constant. Ixidor and that Goblin Chieftain wouldn’t be doing anything this turn, and the game state would only change by the life totals. Even so, Reynolds brought up some great points that I was looking to talk off of.

Reynolds mentioned that you can’t know for certain what Akroma will do after you. What we can do is try to figure out what our best move for every move that Akroma makes. Let’s assume Akroma attacks. Should we attack or not? If we don’t attack, we’ll be at 20 life. If we do attack, we’ll be at 15 life. So it seems like our better move if Akroma does attack is not to attack. Let’s assume, then, that Akroma doesn’t attack. If we don’t attack, we’ll be at 10 life. If we do attack, we’ll be at 5 life. So if Akroma doesn’t attack, we’re better off if we also don’t attack.

This seems like a reasonable way to think about this problem, at least in a very limited sense. There are very clearly some things that are wrong with this reasoning within a Magic sense beyond ceteris paribus. As Reynolds pointed out, there’s more to the game than just this one turn. We have to consider the game in a larger scope, so we’re actually repeating this situation over and over each time it’s our turn. Repeated games are a little trickier, so I’ll punt on that. Another point he brought up is that life isn’t the only factor here; even if we assume that all else remains constant, your choice clearly influences the opinions around the table, so it’s a little complicated. The biggest violation I made here to canon, though, is that Akroma will know what you chose to do when you make a choice. Fortunately, for the idea I’m trying to get across right here, it really doesn’t matter.

What this really is is a Magic setup for the classic problem, the prisoner’s dilemma. Here’s the description on wikipedia:

Two suspects are arrested by the police. The police have insufficient evidence for a conviction, and, having separated both prisoners, visit each of them to offer the same deal. If one testifies (defects from the other) for the prosecution against the other and the other remains silent (cooperates with the other), the betrayer goes free and the silent accomplice receives the full 10-year sentence. If both remain silent, both prisoners are sentenced to only six months in jail for a minor charge. If each betrays the other, each receives a five-year sentence. Each prisoner must choose to betray the other or to remain silent. Each one is assured that the other would not know about the betrayal before the end of the investigation. How should the prisoners act?

Isn’t that grim? This is pretty famous. If you’ve played Baldur’s Gate 2, a genie in the beginning poses it to you. I remember in Dilbert that they split up a bunch of characters into rooms to try to get them to rat each other out for murder. Dilbert very heroically and indignantly points out that since every one of them is on the same side, everyone will shut up and that it won’t work, only to have the blinds pulled up and see that everyone else blames the murder on him.

Dilbert, in this case, is the sucker. It seems like a very attractive option to not betray anyone else; if everyone does that, everyone gets a lighter sentence. The bad news is that even if you convince everyone else to shut up, it’s still better for you to rat them out. Tattling (or not attacking Phage) is an example of a dominant strategy (real Game Theory term). A strategy dominates another strategy if it results in a better outcome for you regardless of how your opponents act. In this case of this Magic game, not attacking dominates attacking because whether Akroma attacks or not, your life total is still higher when you don’t attack than if you do attack.

Obviously, there’s a lot more going on in this situation. Potential take 3 here if you guys come up with more observations about this situation.

Posted in Game Theory | No Comments »

You Make the Play: Star Edition

Saturday, July 18th, 2009

It seems pretty common among magic blogs to offer up situations and get responses on the proper way to play it. So I’m going to do the same thing.

Let’s say you’re playing a magic game in the star format. In this one, there are 5 players, and each player has to try to defeat the 2 people sitting across from them. The first person to do that wins. One of your opponents is Phage, and their opponents are you and Akroma. The board is pretty developed, and choices here matter a lot. Particularly, you and Akroma are both in good positions to attack someone. Your situations are actually pretty similar.

If you both attack Phage, you can probably beat Phage down pretty badly so that she can’t counter attack as strongly. When it comes around to both of your next turns, you’ll both be at 15 life after taking a little hurt from Phage. If you attack Phage and Akroma doesn’t, then Phage will get beat a little, but she’ll be able to counter-attack, and since you attacked her, she’ll hit you back. So you’ll be at 5 life, and Akroma will be at 20 life. Conversely, if you don’t attack and Akroma does, Akroma will be at 5, and you’ll be at 20. If neither of you attack, Phage will just attack both of you, and you’ll both be at 10 life.

It’s your turn, and Akroma’s after yours. Do you attack or not?

(Edit: I guess an even better question is, in addition to how you attack, what else would you do and what factors caused you do choose to do what you did?)

Posted in Game Theory | 1 Comment »

Alpha-Beta Pruning

Sunday, July 12th, 2009

Two weeks ago, I wrote about search in a search tree. The idea was that a game (like Magic) can be broken up into a series of positions, and a good way to determine the best strategy is to evaluate all of these positions and find a path that gets you to a winning state, even when your opponent makes their best move as well. I left a few holes in that article, including how one turns the evaluation function into rules about what to do and what other shortcuts one can find in searching over this very large tree. So let’s finish that.

I briefly mentioned minimax at the end of the last article, and that’s where I’m going to start. Minimax is a strategy for evaluating these trees that should be fairly intuitive. How do players usually make decisions? Based on which outcomes are mostly likely to allow you to win. When you can look at the entire depth of a tree from your current position (as in, you can see every possible way that you win or lose), then you’re trying to reach one of those winning states. To have that happen, you probably need to make a choice on that second to last position to win. But you can also assume there that your opponent is going to make a choice one position before that that tries the most to keep you from winning. What this means is that you can guess at how a game is going to go, and how good a position is by propagating the alternating best and worst positions for you.

Let’s make that more concrete. You are at 2 life, have 2 Ashenmoor Gougers and a summoning sicknessed mogg fanatic in play before your combat step and no cards in hand.  Your opponent is tapped out with a foul imp untapped, 1 foul imp tapped, no cards in hand, and is at 5 life*. What do you do?

It should be fairly obvious that you swing with both gougers and then pop the fanatic for the kill. So let’s see how you came to that.

Your current position is listed above and you’re in your declare attackers step. Your choices are attack with 0, 1, or 2 gougers, each of which represents a different branch from your current position. If you attack with 0 gougers, nothing happens. The next major choice (I cheat a lot since magic has tons of intermediary positions for phases changes and such) is your opponent’s attack step. We assume your opponent is rational and makes his best move, which is to kill you. Technically, he could’ve done nothing during his attack step, but we won’t count on that. So you lose. We can propagate losing up a level to say that not attacking results in you losing.

The same applies for attacking with 1 gouger. You can do that, so the next position to evaluate is how your opponent blocks. He can either block with his imp, or not. Since he’s rational, he sees the lookahead 1 move to where you pop your fanatic and determines that the result of not blocking is losing, and blocking is winning. So he should choose to block, so this position for you can be generalized as a loss.

But if you attack with both, all moves for him result in losing. Thus, that can be propagated to say that your current position is a winning on because the best outcome out of all the possible next positions is a win.

So that’s minimax in its complete form. As I mentioned in the previous post, though, it’s often unfeasible to enumerate the entire tree to the end of the game. Instead, one might look maybe 5 moves ahead and consider all of those possibilities. Since these don’t have definite win/loss states, we can instead use the evaluation function to give them numerical values. We can using the same propagation method to assign the values for positions 4 moves ahead by considering the values of the 5-ahead states that it’s linked to. We can continue to work backwards until we’ve figured out the values for the next move, then pick the best one.

Even so, this is slow. So here’s where alpha-beta pruning comes in. Alpha-beta pruning applies a heuristic to minimax to avoid looking at entire trees. The basic idea here is that we don’t need to consider entire subtrees (all of the positions following a given position) if we know that that subtree can be skipped. From any position, you’re basically doing a lookahead 2 positions to see if you’re in a better spot after your opponent makes their choice. Since we can find maximums and minimums along the way, certain subtrees don’t matter as they’re already less optimal. That was ambiguous; let’s take a trivial example.

Let’s say your opponent has a prodigal pyromancer in play but with summoning sickness. It’s your turn, you have 1 life, and you know your opponent has a goblin piker on the top of their library because you excommunicated it with no cards in hand. You have a lightning bolt and goblin piker in hand with only enough mana for one of the spells, with your opponent at 6 life. From this position, you have 4 choices: bolt the pyromancer, bolt your opponent, make your opponent discard a card, or do nothing. So we can consider these each as a different path down the search tree.

The first is to bolt the pyromancer. If you do this, your opponent’s board is clean. Next, it’s your opponent’s move. They’re only options are to either play or not play their piker. If they play it, your evaluation function puts it at -10, while if they don’t play it, you’re at -5. Since your opponent is trying to minimize your evaluation function, they will play, so the action of bolting the pyromancer has a net value of -10.

The next is to bolt your opponent. If you do this, your opponent is now at 3. On their turn, they can poke with the pyromancer or not, play the piker or not. If they poke you, you die, resulting in an evaluation of -1000. Here’s where alpha-beta pruning comes in. At this point, you know that the action of bolting the pyromancer results in a worst case of -10. Bolting your opponent results in at least a worst case of -1000. There’s a chance that other actions your opponent will make will be worse (probably not), but that doesn’t matter because if you bolt your opponent, one of your opponent’s action is worse than the worst case of another action. So you don’t need to worry about considering the cases where they play the piker and so forth. This is the pruning action of not considering this sub-tree.

This example is a little trivial, but it’s hopefully very clear. Alpha-beta pruning can be used at multiple levels. For example, the position we discussed above might be 3 levels deep in another tree rooted at what you’re actual position is, and the result of that will propagate into a larger situation.

Hopefully, this all seems intuitive. Indeed, we as humans actually prune a lot more deeply than this; in a game, it would never have crossed my mind to not bolt the pyromancer, but those are other heuristics. Maybe that’ll come up in a future post. In the mean time, you can google around for alpha-beta pruning and get more rigorous explanations of how it works and why it’s actually called alpha-beta pruning.

*You’ll note I cheated majorly and made sure that no one has any tricks because minimax, in its most naive form, assumes perfect information. Maybe I’ll deal with this later

Posted in AI, Game Theory | 1 Comment »

M10 Prerelease

Saturday, July 11th, 2009

I just got back from the M10 prerelease and am writing this article in spurts in-between resting while practicing tuba. This really has nothing to do with the class, but now that I have a magic blog, I figured I’d write about it anyways.

My prerelease was a 6-pack sealed, and I ended up going 1-3. Yeah, it was bad. I put together a W/U deck that was relatively quick. It had a soldiers sub-theme with 4 soldiers, which actually appeared a couple times and worked pretty well. I had mid-costed fliers, with my most expensive creatures being 2 serra angels. I think it was an okay deck, and I think I picked the right colors. I had 6 green creatures, 7 red creates, 6 black creatures, 7 blue creatures, and 10 white creatures, so I had to play white. After that, my green and black were the first ones cut (which is a little sad, since green is really good, but I’ll get to that). In the end, I didn’t have enough depth in red, so I went blue. I 2-0ed in my practice. I won my first game decisively, lost my second game to an overrun, and lost the third game to another overrun where he would’ve been dead had he not killed me with exactly 19 points of damage. It was unfortunate, but definitely my fault, as I made a very serious play mistake in forgetting what I saw with a sage owl. So lost 1st round and then lost both games in my 2nd round to overruns. Third round, I had to mulligan to 5 for having no lands, then didn’t get my colors right, and lost the 2nd game in a pretty good fight. 4th round, I won the first game decisively, lost the second game decisively, and won the third game decisively. So green is very good. Each of my opponents played some green, so it’s good

So with that overview, here are some comments on specific cards:

– wall of frost: very good. I didn’t get to play him a lot, but he’s good like wall of denial.

– rod of ruin: also good. There are a lot of 1 toughness creatures around, and repeatable removal is good

– terramorphic expanse: good, but not really necessary. Not once was I in color trouble that I needed it to save me. On the otherhand, it was never a drawback. I never wished I had a real land on a turn I dropped it. Middle to low pick

– serra angel: it’s amazing. At uncommon, you’ll see a lot of these floating around, and if you’re playing an aggressive white/X deck, this is a great card to have at the top of the curve. Only deadly recluse and another serra angel were good enough to intimidate it into not attacking. Very high pick

– blinding mage: good, but not what I was hoping. I know it should be good, but it didn’t get me out of trouble as much as I was hoping. My deck had a very good curve, so I often didn’t have the mana open to use it, but I’d still draft him high

– righteousness: much better at uncommon than rare. It worked a couple times, so I believe in it

– rhox pikemaster: a lifesaver. This card is great. I saw a lot of deathtouch and mid-sized creatures, and this makes all your soldiers so much better than them. High pick

– veteran swordsmith: very good, but not quite what I was hoping. Of course, if you’re going for a soldier theme, use it, but the 1 power generally didn’t matter that much. I think the 1 toughness would’ve been much better.

– safe passage: fantastic combat trick. Get it while you can

– elite vanguard: very good. Not surprising that savannah lions is good, but I got him 1st turn a couple times, and quite a few of my opponents didn’t have plays until turn 3. He’ll get in some damage, and if you have other soldiers to boost him, it can still be useful midgame

– ice cage: I thought about crystallization when I saw this card. It’s like crystallization, but so much worse. With blinding mage, prodigal pyromancer, and rod of ruin around, it just always feels delicate. Against green, they’re going to cast giant growth or oakenform on their creatures anyways, so that’s no help. The removal in other colors is just much better (I would’ve absolutely taken pacifisms had I opened any), so use that instead.

– mind control: very good.

– sage owl: amazing. It seeemed like I always wanted to smooth out my mana draws, and that’s exactly what the owl can do. But you should really take notes about what you see, or like me, you’ll make a mistake because of what you think you have coming up

– illusionary servant: see ice cage. It’s good, but not as good as some people I’ve heard talk about it. It did win me one game because my opponent didn’t understand it, but otherwise, it sat in my hand a lot because I knew it was dead on arrival

– sleep: It’s all that and more. Take it and play blue just to use it. This was the best finisher ever. In a lot of games I played, the board just got swamped as no one wanted to attack into the other, hence why overrun crushed me a couple times. On the other hand, sleep can do it, too. If you have 10 power of creatures, it’ll go all the way for you. Especially combined with…

– silence: mostly not a good card, except for the turn before you’re going to alpha strike. Especially played during upkeep after you play sleep, it can be useful.

– time warp: meh. It was good with sleep as well, netting you 3 free attacks, but that’s hard to do, since you need a lot of mana. Cool card, not amazing.

– solemn offering: didn’t need to use it, or naturalize. I didn’t play a single game where I needed artifact/enchantment destruction. Good to have in the board, and not worthy of a slot.

– overrun: better than sleep. This card just destroyed me each time. This will win games for you, so draft it when you see it and use it often. Combine with howl of the night pack for a really dirty win.

– deadly recluse: awesome. It stopped me a lot from attacking with my much more valuable fliers. And that 2 toughness is actually a lot. I see this as a solid middle pick.

Hope it helps.

Posted in Random | No Comments »

Two Kinds of AI (extended)

Thursday, July 2nd, 2009

One of the Magic blogs I watch is one from a guy writing a Magic program called Forge. It’s all written in java using swing stuff, and for just one guy, it’s pretty impressive. It’s got a fairly large card library and decent AI with lots of wingdings and features like drafting and a quest mode. Unlike a lot of magic programs that depend on the players to enforce rules, it actually has a concept of phases and the flow of the game. Props.

He (I’m assuming he; sorry if that’s incorrect) made  a fairly interesting post today about 2 types of AI. The first he describes is where each card has certain rules associated with it, and based on these bits, it comes up with a plan. The other is a mathematical where various cards are weighted and plays are evaluated (like I described in earlier posts). Forge uses the former, while Duels of the Planeswalker deals with the latter. I figured I would expand on this some.

What he’s describing is actually a fairly important divide in AI right now. AI can be split into two general categories: symbolic AI and statistical AI, with symbolic being the specific knowledge and statistical being the weighting of cards. Right now, AI is actually heavily skewed towards statistical AI, mostly because it works. Symbolic AI matches better with how we think humans work: it has concepts and some knowledge coded in. It, however, hasn’t delivered. The big successes in AI recently have been with a statistical approach. For example, web search (like google) is an AI problem; given a set of query words, try to send back meaningful links. It would be very difficult to actually come up with specific meanings for the crazy number of websites out there. Instead, methods like data mining can apply statistical methods to draw connections from millions of examples.

Of course, the boundary isn’t strict. Take the “related videos” in youtube. They’re mostly generated by analyzing tons of videos, figuring out what people watch after their current video, relative ratings, and so on. An important part to that, though, is determining the presence of tags and similarities between videos. For example, the tags “batman” and “superman” are more likely to indicate similarity between 2 videos than “batman” and “carrots.” Of course, this analysis is also a part of the huge mathy cog that is data mining, but at some level, it’s backed by some representation of knowledge, even if it’s just a word inputted by the user to describe the video.

I’m not yet willing to hedge my bets on whether one is better than the other. So far, statistical AI has proven very useful, but I actually spent last summer working with a cognitive architecture to generate football plays. It’s amazing how logical inference and reasoning can take some simple things, such as moving a player around, and demonstrate some idea of trying to find gaps. One of the big obstacles is trying to demonstrate general intelligence instead of relying on domain specific knowledge. Like the Forge programmer mentioned, he writes blurbs specifically for giant growth or shock. The first step for a reasoning agent would be to generalize shock logic to incinerate. Trying to use that to play chess is another entire matter, but small steps might one day yield some crazy emergent qualities, and that AI would be something that truly understands what it’s doing.

Posted in AI | 1 Comment »

Magic Designers on 2010 Rules Changes

Wednesday, July 1st, 2009

For an interesting perspective on the rule changes in Magic 2010 and Duels of the Planeswalker, you might want to check out this podcast with 2 of the original designers of Magic, Richard Garfield and Skaff Elias, and another game designer, Tyler Bielman. None of them are as heavily involved with Magic nowadays, having seemed to mostly move on, but it’s interesting to hear the difference between the original intent and design of the game and what’s happened to the game and its rules since. threedonkeys.com/blog is a legit blog with both posts and podcasts, so you might want to get a feed or monitor it if you’re interested in game design in general.

Posted in Game Design | No Comments »